Satellite TV - Scientific Analysis

3 A Fixed Dish

To recap, three settings (parameters) together completely describe the alignment of a fixed dish:

Azimuth, the horizontal angle in degrees measured clockwise from True North;

Elevation, the vertical angle in degrees measured upwards from the horizontal;

Skew, the polarisation angle of the incoming signal, clockwise positive viewed from behind the dish.

All these values are completely determined by:

Longitude difference, DLong, including sign, between the target satellite and the dish site

Latitude, Lat, of the dish site

Because it depends on whether longitudes are west (-ve) or east (+ve), and latitudes south (-ve) or north (+ve), azimuth is rather unwieldy for the purposes of this discussion. Consequently, a more convenient intermediate result in its calculation is used here, the apparent difference in longitude (DLongA), defined as the angle east or west of the dish site's meridian at which the target satellite appears. The actual relationship between the two is:

Azimuth =	DLong -ve	DLong Zero	DLong +ve
Lat -ve	DLongA	0	360 - DLongA
Lat Zero	90	0	270
Lat +ve	180 - DLongA	180	180 + DLongA

Azimuth =

DLong -ve

DLong Zero

DLong +ve

Lat -ve

DLongA

360 - DLongA

Lat Zero

270

Lat +ve

180 - DLongA

180

180 + DLongA

All these angles are marked on the following diagram:

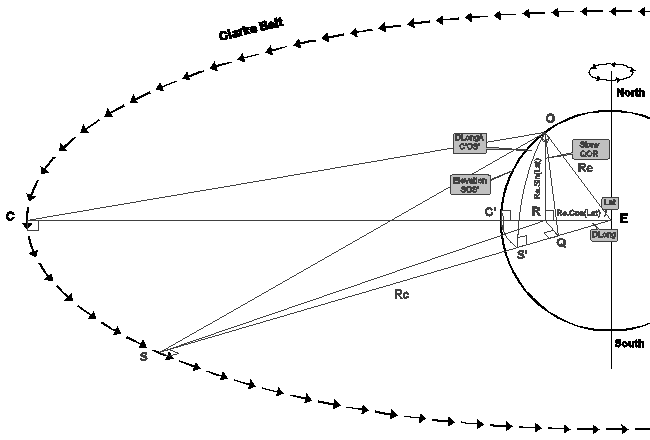
The settings can be derived as follows ...

Consider the spherical triangle OC'S':

	Sin(DLongA) Sin(DLong)	=	Sin(OS'C') Sin(Lat)	Spherical Sine Law (18)
∴	Sin(DLongA)	=	Sin(DLong).Sin(OS'C') / Sin(Lat)
&	Cos(DLongA)	=	-Cos(OC'S').Cos(OS'C')+Sin(OC'S').Sin(OS'C').Cos(DLong)	Spherical Cosine Law (19)
∴	Cos(DLongA)	=	Sin(OS'C').Cos(DLong)	OC'S' = 90°
∴	Sin(DLongA) Cos(DLongA)	=	[Sin(DLong).Sin(OS'C')] [(Sin(Lat).Sin(OS'C').Cos(DLong)]	Divide first result by the second
∴	Tan(DLongA)	=	Tan(DLong)/Sin(Lat)	Tan(A) = Sin(A)/Cos(A)
∴	DLongA	=	ArcTan[ Tan(DLong) / Sin(Lat) ]

Consider again the spherical triangle OC'S':

	Cos(OES')	=	Cos(DLong).Cos(Lat) + Sin(DLong).Sin(Lat).Cos(OC'S')	Spherical Cosine Law (11)
∴	Cos(OES')	=	Cos(DLong).Cos(Lat)	OC'S' = 90°

Consider the triangle EOS:

	SO²	=	Rc² + Re² - 2.Rc.Re.Cos(OES)	Cosine Law
∴	SO	=	√[Rc² + Re² - 2.Rc.Re.Cos(OES)]
&	Sin(EOS) / Rc	=	Sin(OES) / SO	Sine Law
∴	Sin(EOS)	=	Rc.Sin(OES) / SO
∴	Sin(EOS)	=	Rc.√[1 - Cos²(OES)] / SO	Cos²(A) + Sin²(A) = 1 (5)
∴	Sin(EOS)	=	Rc.√[1 - Cos²(OES)] / √[Rc² + Re² - 2.Rc.Re.Cos(OES)]	Substitute SO
∴	Sin(EOS)	=	Rc.√{ [1 - Cos²(OES)] / [Rc² + Re² - 2.Rc.Re.Cos(OES)] }
∴	Sin(EOS)	=	√{ [1 - Cos²(OES)] / [1 + (Re/Rc)² - 2.(Re/Rc).Cos(OES)] }	Divide through by Rc
∴	Sin(EOS)	=	√ [1-Cos²(DLong).Cos²(Lat)] [1+(Re/Rc)²-2.(Re/Rc).Cos(DLong).Cos(Lat)]	Substitute Cos(OES) = Cos(OES')
&	EOS	=	90 + Elevation	By definition
∴	Sin(EOS)	=	Sin(90 + Elevation)
∴	Sin(EOS)	=	Sin(90).Cos(Elevation) + Cos(90).Sin(Elevation)	Compound Angles (1)
∴	Sin(EOS)	=	Cos(Elevation)
∴	Cos(Elevation)	=	√ [1-Cos²(DLong).Cos²(Lat)] [1+(Re/Rc)²-2.(Re/Rc).Cos(DLong).Cos(Lat)]
∴	Elevation	=	ArcCos ( √ [1-Cos²(DLong).Cos²(Lat)] [1+(Re/Rc)²-2.(Re/Rc).Cos(DLong).Cos(Lat)] )

Consider the triangle EQR:

	QR	=	ER.Sin(DLong)
∴	QR	=	Re.Cos(Lat).Sin(DLong)	Substitute ER
&	Tan(Skew)	=	QR / OR	Definition of Tan
∴	Tan(Skew)	=	Re.Cos(Lat).Sin(DLong) / Re.Sin(Lat)	Substitute QR & OR
∴	Tan(Skew)	=	Sin(DLong) / Tan(Lat)	Tan(A) = Sin(A)/Cos(A)
∴	Skew	=	ArcTan[ Sin(DLong) / Tan(Lat) ]

The following tables show examples of DLongA, Elevation, and Skew:

Apparent Difference In Longitude (DLongA)
Latitude (Lat)	Actual Difference In Longitude (DLong)
Latitude (Lat)	0	10	20	30	40	50	60	70	80	90
0	0.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00
10	0.00	45.44	64.49	73.26	78.31	81.71	84.27	86.38	88.25	90.00
20	0.00	27.27	46.78	59.36	67.82	73.99	78.83	82.90	86.55	90.00
30	0.00	19.43	36.05	49.11	59.21	67.24	73.90	79.69	84.96	90.00
40	0.00	15.34	29.52	41.93	52.55	61.66	69.64	76.83	83.53	90.00
50	0.00	12.96	25.41	37.00	47.61	57.27	66.14	74.42	82.31	90.00
60	0.00	11.51	22.80	33.69	44.10	53.99	63.43	72.50	81.32	90.00
70	0.00	10.63	21.17	31.57	41.76	51.74	61.52	71.12	80.59	90.00
80	0.00	10.15	20.28	30.38	40.43	50.43	60.38	70.28	80.15	90.00
90	0.00	10.00	20.00	30.00	40.00	50.00	60.00	70.00	80.00	90.00

Notes

DLong and DLongA only agree at 0° and 90° and at the poles;
On the equator, any satellite that is not directly overhead must lie either east or west;
At intermediate latitudes DLongA always lies between these limits.

Elevation
Latitude (Lat)	Actual Difference In Longitude (DLong)
Latitude (Lat)	0	10	20	30	40	50	60	70	80
0	90.00	78.23	66.55	55.03	43.72	32.69	21.93	11.47	1.30
10	78.23	73.42	63.92	53.34	42.58	31.89	21.40	11.15	1.15
20	66.55	63.92	57.32	48.74	39.32	29.60	19.84	10.19	0.69
30	55.03	53.34	48.74	42.15	34.39	26.01	17.36	8.63	0.05
40	43.72	42.58	39.32	34.39	28.28	21.40	14.08	6.55
50	32.69	31.89	29.60	26.01	21.40	16.05	10.19	4.02
60	21.93	21.40	19.84	17.36	14.08	10.19	5.82	1.15
70	11.47	11.15	10.19	8.63	6.55	4.02	1.15
80	1.30	1.15	0.69	0.05

Interchangeable symmetry between Lat and DLong in the formula results in diagonal symmetry in the table.

Skew
Latitude (Lat)	Actual Difference In Longitude (DLong)
Latitude (Lat)	0	10	20	30	40	50	60	70	80	90
0	0.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00	90.00
10	0.00	44.56	62.73	70.57	74.66	77.04	78.49	79.37	79.85	80.00
20	0.00	25.51	43.22	53.95	60.48	64.59	67.20	68.83	69.72	70.00
30	0.00	16.74	30.64	40.89	48.07	53.00	56.31	58.43	59.62	60.00
40	0.00	11.69	22.18	30.79	37.45	42.39	45.90	48.24	49.57	50.00
50	0.00	8.29	16.01	22.76	28.34	32.73	36.01	38.26	39.57	40.00
60	0.00	5.73	11.17	16.10	20.36	23.86	26.57	28.48	29.62	30.00
70	0.00	3.62	7.10	10.31	13.17	15.58	17.50	18.88	19.72	20.00
80	0.00	1.75	3.45	5.04	6.47	7.69	8.68	9.41	9.85	10.00
90	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Skew is only zero at the poles and on the meridian
On the equator, any satellite that is not directly overhead will have a skew of ±90°
At intermediate latitudes Skew always lies between these limits

Note: Sometimes where it is useful to illustrate a point, tables in this and the following page may include data for when a satellite would actually be invisible below the horizon.