Satellite TV broadcasts are received from ground stations by orbiting satellites and retransmitted back down to a target area, usually a particular country or group of countries.
It has advantages of reliability over terrestrial TV - there is fault potential of just one sat between signal source and destination, versus a network of transmitters all exposed to local weather hazards (though today transmitters are often fed by satellite rather than another transmitter upstream). However, both can be affected by weather, and neither achieves complete coverage - both can be blocked by local obstructions such as buildings or trees, while terrestrial might not be receivable in steep sided valleys and gorges, satellite on steep slopes facing away from the equator.
Only satellites in 'geo-stationary' orbit are suitable for public broadcasting. This orbit is ...
... and consequently from Earth a satellite in this orbit appears stationary in the sky, enabling members of the public to receive broadcast TV using a relatively simple fixed dish.
Scientists had proposed the concept of geo-stationary orbit since the turn of the 19th and 20th centuries, but Arthur C Clarke, best known for his science fiction such as '2001 A Space Odyssey', was the first in the space era to publish, writing in an article for 'Wireless World' in 1945. Consequently, the orbit is also known as a Clarke Orbit, a satellite in it as a Clarke Satellite, and, most commonly, the ring of geo-stationary satellites circling the equator as the Clarke Belt. Here, the term 'satellite' will always refer to a Clarke Satellite.
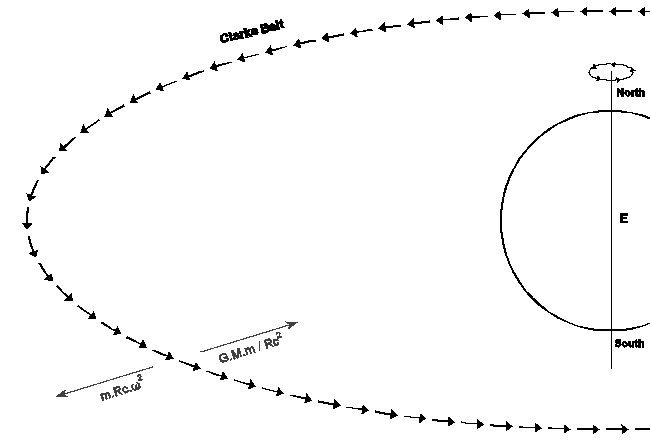
The calculation of a Clarke Orbit derives from Newton's work and simply balances the gravitational force on a satellite against its centrifugal effect (inertial tendency to carry on in a straight line, requiring a constant inward force to maintain circular motion), and is reproduced below:
| Gravitational And Earth Constants: | ||||
|---|---|---|---|---|
| Gravitational Constant | G | = | 6.67E-20 | km³ / kg s² |
| Equatorial Radius Of Earth | Re | = | 6.38E+03 | km |
| Mass Of Earth | M | = | 5.98E+24 | kg |
| Sidereal Day Length | D | = | 8.62E+04 | s |
| Angular Velocity Of Geo-Stationary Satellite | ω | = | 2.π / D | Rad / s |
| = | 7.29E-05 | Rad / s | ||
| Let Be: | ||||
| Mass Of Satellite | m | kg | ||
| Radius Of Clarke Belt | Rc | km | ||
| Clarke solution sets centrifugal effect equal to gravitational force: | ||||
| m.Rc.ω² | = | G.M.m / Rc² | ||
| ∴ | Rc.ω² | = | G.M / Rc² | |
| ∴ | Rc³.ω² | = | G.M | |
| ∴ | Rc³ | = | G.M / ω² | |
| ∴ | Rc | = | ³√( G.M / ω² ) | |
| Therefore Radius Of Clarke Belt | = | 42,164 | km from centre of Earth | |
| = | 26,353 | miles | ||
| = | 35,786 | km above surface of Earth | ||
| = | 22,366 | miles | ||