Satellite TV  -  Scientific Analysis

4  An H-H Rotor

To receive signals from anywhere in the sky, a dish must move both horizontally and vertically, and some can do that.  However, to track the Clarke Belt, they are somewhat overkill  - a simpler and cheaper assembly of a dish rotating around a single axis does almost as well.

The realisation crucial to understanding this possibility is that the radius of Earth, 6378km, is comparatively small compared with the radius of the Clarke belt, 42164km, so anyone on the surface of Earth is 'almost' at the centre of the Clarke belt.  Thus, a dish mounted on an axis approximately perpendicular to the equatorial plane of the Clarke Belt, and pointed initially at the nearest point of it, as it turns around this axis will cover a great many of the nearest 'visible' sats before the error from not actually being at the centre becomes significant.

That is how an H-H Satellite Rotor works.  The principle is illustrated in the following diagram ...

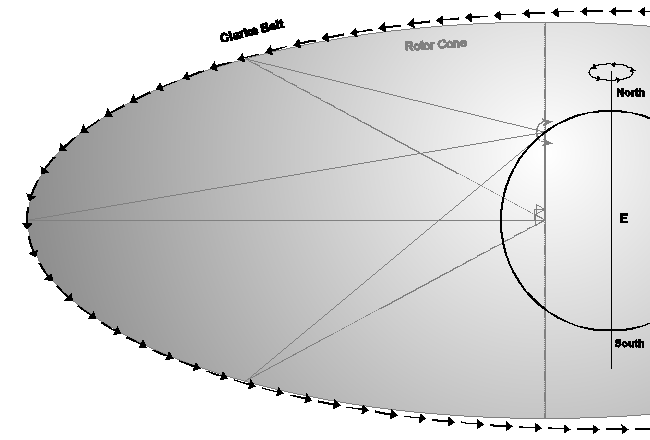
However, the simplicity of the principle is easily lost amid practical complexities ...

Many of the angles in a practical dish system do not contribute to its central purpose, they are there merely for convenience, mostly of manufacture and installation:

• Offset dishes avoid the LNB shading a significant area of the dish, and allow mounting nearer to vertical against the wall of a house, thus being less prone to wind damage, less of an obstruction, and less noticeable;
• Mounting adjustments allow fixed dishes to cover a range of longitudes and latitudes;
• Rotor cranks allow normal fixed dishes to be mounted on rotors without special mountings or extreme adjustment ranges;
• Rotor tilt adjustments allow rotors to cover a range of latitudes.

But here forget the complexities of the installation setting angles.  Once it is all bolted together and installed, it's two rigid structures connected by the pivot of the rotor spindle, and the Pivot Rule implies that either side of this pivot all that matters is the net angles involved.

In demonstration, partially straighten a paperclip leaving some bends, and rotate one end between your fingers.  You'll see that the other end remains at a constant angle to the one's axis of rotation, and, like a lighthouse beam, depending on how you bent the clip downwards, horizontal, or upwards, it sweeps out the surface of a cone, as illustrated above, or of a disc.

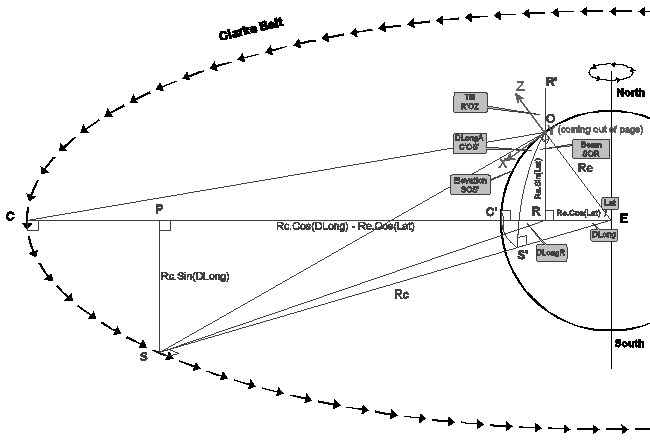
In principle then, the only three angles that matter are ...

1. Tilt angle, that the rotor axis OR, that is the line of its bearings, makes with respect to Earth at the dish site, sometimes measured from the vertical R'OZ (90 − Latitude), sometimes the horizontal (Latitude)  -  the site's latitude and this setting in combination leave the axis parallel to the poles, perpendicular to the equatorial plane of the Clarke Belt, or nearly so;
2. Beam* angle, made with that axis, depending on context, either SOR by the incoming sat signal SO, or by the sum of the setting angles on the dish side of the rotor  -  crank angle (−ve), dish elevation (+ve), and offset (+ve), though the latter two will probably be combined into a single dish elevation setting (+ve);
3. DLongR the rotational longitude difference, SRP, that the rotor turns to point to a sat at DLong, aka the Polar Mount / Rotor Hour Angle, in the Calculator page as Rotor Azimuth.

* Many instead use Declination, particularly referring to the nearest point of the Clarke Belt where unambiguously it's OCE = OCR = 90−Beam, but anywhere else, there's potential ambiguity between OSE and OSR.

The following tables give examples of DLongR and Beam (defined here as the angle SOR between an incoming sat signal SO, and a rotor axis OR perpendicular to the Clarke Belt):

Note that:

• As with DLongA, DLong and DLongR only agree at the North or South Pole or when both are zero
• Elsewhere DLongR is always greater then DLong, the maximum difference being on the equator

Results are classified to reflect the common rotor ranges.  Note that:

• Worst case variation (bold) is near Latitude 40°, 0.21° for a ±40° rotor, 0.42° for a ±60° rotor.
• As might be expected, the minimum and maximum for each range are at the extremes of the range (for example, for the 0-40° range the minimum is at DLong = 0° and the maximum at DLong = 40°).
• The 'midrange' shown for each range is the average of the maximum and minimum over that range.

When setting up the rotor, the error in DLongR tracking around the Clarke Belt is a given, unalterable feature of the rotor.  Most rotors step through divisions of 0.1°.

However the Beam setting can be optimised by using the midrange value shown above for the rotor's range.  This halves the intrinsic error to 0.11° for a ±40° rotor and 0.21° for a ±60° rotor.

Although this seems common sense, actually proving it is not straightforward and requires vector manipulation with matrices.  Although much work, it yields a powerful analytical tool.

The following table lists intrinsic rotor error over both common ranges, assuming:

• Rotor axis exactly perpendicular to the Clarke Belt
• Dish elevation sets the given beam angle (midrange as above for rotor range and site latitude)
• Rotor angular step resolution of 0.1°

Note that:

• Even on the equator, the limit of the rotor step angle introduces some error.
• For these conditions, in theory these are optimal results; in reality installation errors will dominate  -  the best possible accuracy with most rotor and dish scales ≈0.1°, it's difficult to avoid slight movements as bolts are tightened, dishes tend to distort slightly under their own weight, etc.

Some sites give rotor tilts leaning slightly forward from perpendicular towards the Clarke Belt.  Depending on rotor range and latitude, such 'forward' tilts can significantly reduce the intrinsic errors above, as can be gauged using the previous vector analysis.

The following table lists intrinsic rotor error for 'forward' tilts over the same ranges, assuming:

• Rotor axis leaning forward by difference between Beam_DLongR=90 & Beam_DLongR=0
• Dish elevation sets the given beam angle for DLongR = 90°
• Rotor angular step resolution of 0.1°

Practical usefulness will be limited by rotor and dish scale accuracy, and may be doubtful for ±40° rotors, perhaps excepting mid-latitude problem systems, but more probable for ±60° rotors.